A spherical balloon of radius 15 feet subtends an angle 60∘ at the eye of an observer. If the angle of elevation of its center is 45∘, find the height of the center of the balloon.
Answer:
15√2 feet
- The following picture shows the observer at point A, observing a balloon.
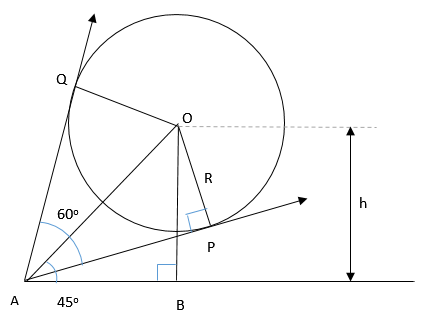
- Let's assume the height of the center of the balloon to be h, therefore OB=h
Also, assume the distance of center of the balloon from observer to be D, therefore OA=D - For triangle △OAP,
sin∠OAP=RD⟹sin60∘2=RD⟹sin30∘=RD⟹12=RD⟹D=2R…(1) - For △AOB,
sin∠OAB=hD⟹sin45∘=hD⟹1√2∘=hD⟹D=√2h…(2) - On equating two values of D from equation (1) and (2),
√2h=2R⟹h=R√2⟹h=15√2 feet
 UAE
UAE


